The famous Monty Hall problem is used by educators to get students to think about the concept of probability and chance. It is often introduced in math probability classes for junior college, polytechnic and university students, and sometimes even in secondary schools.
The problem is as follows: A talk show host presents to a contestant three closed doors. Behind one of the doors is a valuable prize, usually an expensive car, a jewelry set, or some other luxury item. Behind each of the other two doors is a goat or some other object of considerably lesser value.
The contestant first chooses a door he wishes to open. The talk show host then opens another door apart from the contestant’s choice to reveal a goat. The contestant decides whether to switch to the remaining unopened door or stick with his original choice. His final choice is then opened, and the contestant gets whatever is behind the door he has picked.
Is it better for the contestant to switch doors after the talk show host has opened one of them, or to retain his original choice?
The solution to this problem is well known: It is better for the contestant to switch to the remaining unopened door as this will give him a higher probability of winning the valuable prize.
While this problem in probability is easy to state, very often the solution presented to students is far more complicated than it needs to be.
Sometimes, the student will be asked to draw a decision tree to illustrate the various scenarios and their consequences, and to use the decision tree to draw the conclusion that it is better to switch doors. An example of such a decision tree is as follows:
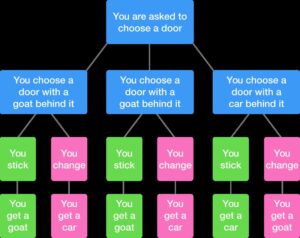
In the above decision tree, it can be easily seen that in two out of the three scenarios depending on whether you initially picked a door which hid a car or a goat, switching to another door will net you the car. In other words, 2 out of 3 times, switching is the correct option. Hence, it is better for the contestant to switch than to retain his initial choice.
Another popular approach is by the use of Bayes’ Theorem, which is taught to polytechnic and university students, and sometimes, in H2 Mathematics enrichment classes. A common method is as follows:
Assume that the contestant has chosen door 1. Let A denote the event that door 1 has a car behind it, and let B denote the event that door 2 is opened by the talk show host. We then compute P(A|B), the conditional probability that door 1 has a car behind it given that the talk show host has opened door 2.
After some working involving Bayes’ Theorem (sometimes taking up to one full page!), it is determined that P(A|B) = 1/3, thus illustrating that retaining the original choice would only lead to a 1/3 probability of winning the car. Changing doors therefore leads to a 2/3 probability of winning the car, and so it is better to change.
However, the use of Bayes’ Theorem or the use of a decision tree obscures the fact that there is a far simpler explanation. Remember that the contestant initially choses one of the doors without any information provided by the talk show host. Since the contestant starts off with no knowledge, his choice is equivalent to a totally random selection. He therefore has a 1/3 probability of picking the correct door with the car. The probability of winning the car will remain at 1/3 if the contestant ignores all additional information presented to him (this is equivalent to him not even knowing that the talk show host has opened another door) and sticks with his original selection. It is thus better for him to change doors.
This explanation avoids invoking Bayes’ Theorem and obviates the need to draw out decision trees. It is so easy it can even be understood by ‘O’ level students studying probability for the first time.


